Introduction
This article provides an in-depth examination of Poly Tubing.
You will explore topics including:
- What Poly Tubing is
- The manufacturing process of Poly Tubing
- Materials used in Poly Tubing production
- Applications of Poly Tubing
- And more...

Chapter One - What is Poly Tubing?
Polyethylene tubing is renowned for being lightweight, flexible, and durable. It's manufactured from various polymers including polyethylene, polypropylene, and polyurethane, which result from ethylene polymerization. This type of tubing is highly versatile with crack-resistant and break-resistant walls. Common varieties include high-density polyethylene (HDPE) and low-density polyethylene (LDPE).
Poly tubing refers to all tubing types made from distinct polymers derived from natural gas and crude oil. Its widespread adoption stems primarily from cost efficiency, with polyethylene being one of the most economical resin options available.

The key difference between HDPE and LDPE lies in their flexibility. LDPE is highly flexible, while HDPE is more rigid. Despite these differences, both types offer similar integrity and durability. Extrusion is the predominant manufacturing method for poly tubing.
Polyurethane, a common resin for poly tubing, can be either rigid or flexible. Originally developed during World War II as a rubber substitute, polyurethane's superior durability and performance led to its increased use during and after the war.
Chapter Two - How Poly Tubing is Made
Poly tubing, also called plastic tubing or poly pipe, is produced from high-performance thermoplastics like polyurethane, polypropylene, and polyethylene. These polymers consist of ethylene chains containing carbon and hydrogen atoms. The raw materials come from crude oil and natural gas, with natural gas being the more common feedstock in modern plastic production. Wall thickness, density, and diameter are carefully customized for specific applications, whether industrial piping, irrigation, medical uses, or flexible packaging. Characteristics like rigidity, flexibility, and clarity are determined by manufacturing adjustments and resin selection, making poly tubing adaptable for various industries.
Poly tubing primarily comes in two types: HDPE (High Density Polyethylene) and LDPE (Low Density Polyethylene). HDPE is rigid with high tensile strength, ideal for durable, chemical-resistant applications like water lines. LDPE offers greater flexibility and transparency, commonly used in plastic bags and protective sleeves. Despite structural differences, both types are initially processed using heat from petroleum products.
Raw Material
Poly tube production begins with polyethylene manufacturing. Polyethylene (PE) is created through ethylene gas polymerization from crude oil or natural gas. As part of the polyolefin family, it ranges from low-density (soft, flexible) to high-density (rigid, robust), each with distinct physical properties and chemical resistance. Polyethylene's molecular structure underpins its performance in applications requiring flexibility, impermeability, and strength.
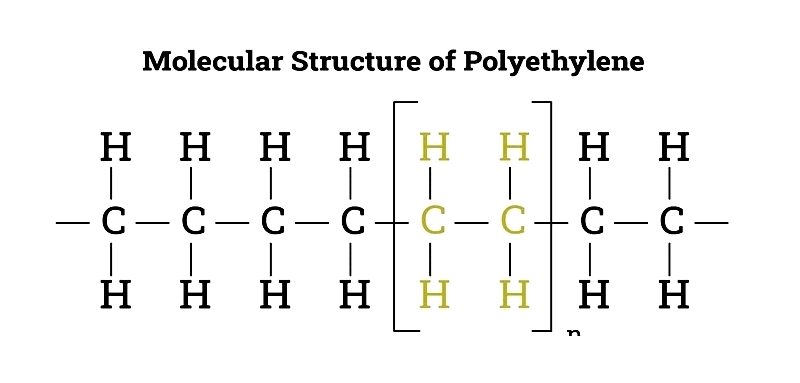
Four primary processes are used in poly tubing manufacturing: extrusion, injection molding, blow molding, and rotomolding. While all begin with heating polyethylene, each produces tubing with different mechanical properties and surface finishes for various commercial and consumer needs.
The chosen manufacturing process significantly impacts poly tubing's real-world performance, affecting flexibility, stress crack resistance, transparency, and chemical/UV resistance. High-quality poly tubing may include additives like UV stabilizers or colorants to meet specifications.
Extrusion
Extrusion is the most common method for producing poly tubing. The process starts with feeding polyethylene resin pellets (sometimes with additives) into a hopper. A rotating screw moves the pellets through a heated barrel, melting them evenly to prevent degradation.
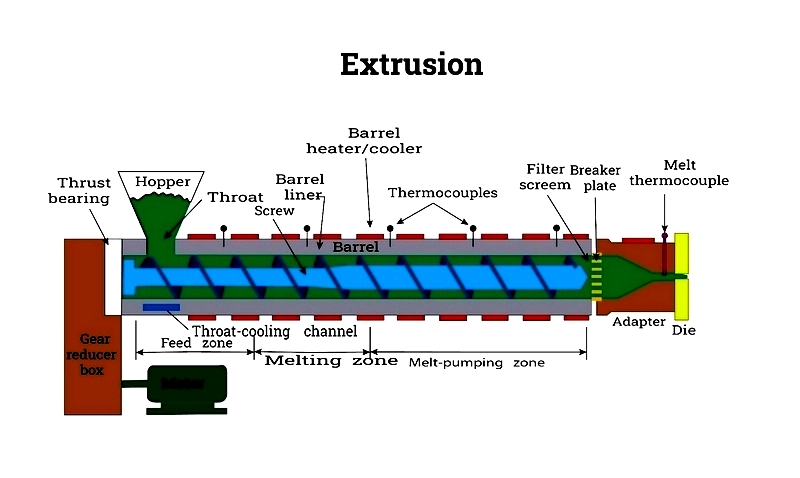
The molten material passes through filters to remove contaminants, then through a die that shapes the tube's dimensions. After extrusion, the tube is cooled in a water bath to maintain its form, then cut to length and possibly treated further.
Extrusion offers high production rates, low costs, and versatility in tube sizes and shapes. It's widely used for irrigation tubing, hydraulic lines, and food-grade tubing.
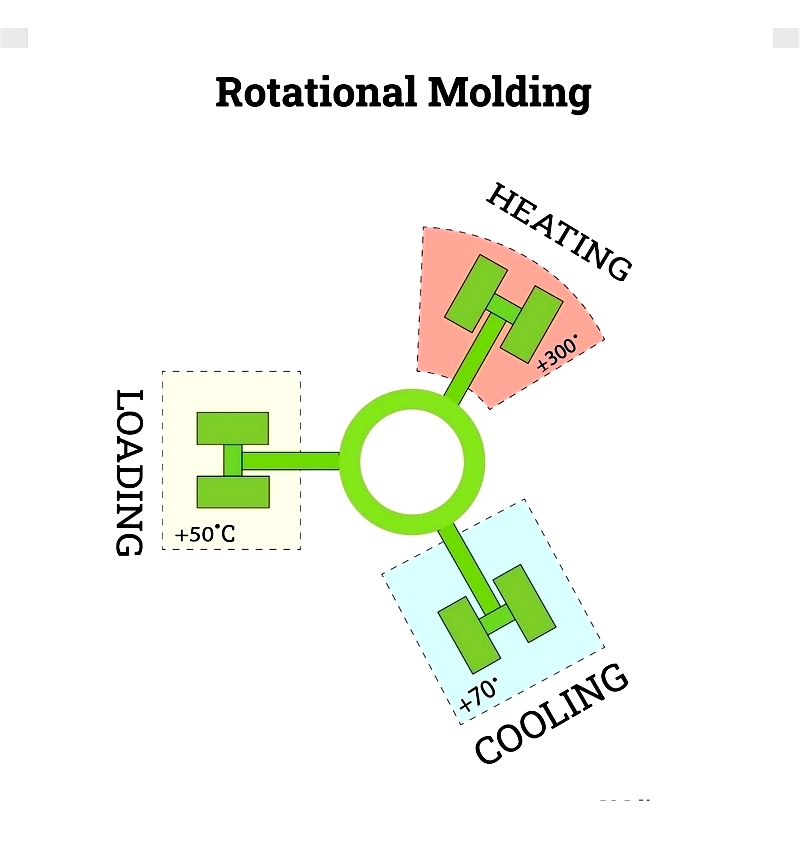
Rotational Molding
Rotational molding (rotomolding) produces large-diameter poly tubes and hollow vessels. Plastic powder is placed in a mold that's heated and rotated, coating the interior evenly. This method creates seamless products with precise wall thickness.
Rotomolding is ideal for custom shapes and low-to-medium production volumes, though it's more labor-intensive than extrusion. Cooling methods maintain dimensional accuracy in the final product.
Pultrusion
Pultrusion combines pulling and extrusion to create high-strength tubing. Heated thermoplastic is pulled through a die over a mandrel, producing straight, consistent tubing. This method allows various diameters and composite configurations for demanding applications.
Pultrusion is used where lightweight, high-strength tubing is needed, such as in aerospace or automotive industries. Related pullbraiding adds braided fibers for extra strength.

When selecting poly tubing for projects, consider materials, production processes, and application requirements. Partnering with experienced manufacturers ensures products meet industry standards for pressure rating and chemical compatibility. The right combination of material, dimensions, and production method maximizes performance and value.
Chapter Three - Top Poly Tube Producing Machines
Poly tube manufacturing is crucial across industries like medical, agriculture, and packaging. Demand for high-quality tubing drives the need for advanced extrusion technology. Below are leading poly tube production machines with their features and advantages.
Model: Davis-Standard DS-SPF
Manufacturer: Davis-Standard, LLC.
Features: The DS-SPF blown film extruder offers versatility and precision for polyethylene tubing. Its control systems ensure consistent thickness and high output rates. Automation and monitoring make it ideal for productivity-focused manufacturers in packaging and industrial tubing markets.
Model: Gloucester Engineering X-SERIES
Manufacturer: Gloucester Engineering Company
Features: The X-SERIES excels in dimensional accuracy and output. Its modular design allows integration with downstream equipment, serving food packaging and medical tube sectors effectively.
Model: W&H VAREX II
Manufacturer: Windmöller & Hölscher (W&H)
Features: The VAREX II provides high-speed production with precise thickness control. It supports multi-layer extrusion and quick changeovers for packaging and medical-grade tubing.
Model: Macchi Coex Flex
Manufacturer: Macchi S.p.A.
Features: The Coex Flex specializes in multi-layer tubing with enhanced barrier properties. Its automated systems meet strict food and pharmaceutical standards.
Model: Leistritz ZSE MAXX
Manufacturer: Leistritz Advanced Technologies Corp.
Features: The ZSE MAXX twin-screw extruder offers superior mixing and throughput for various polyolefins. It's suitable for both R&D




